
Heap : Priority Queue
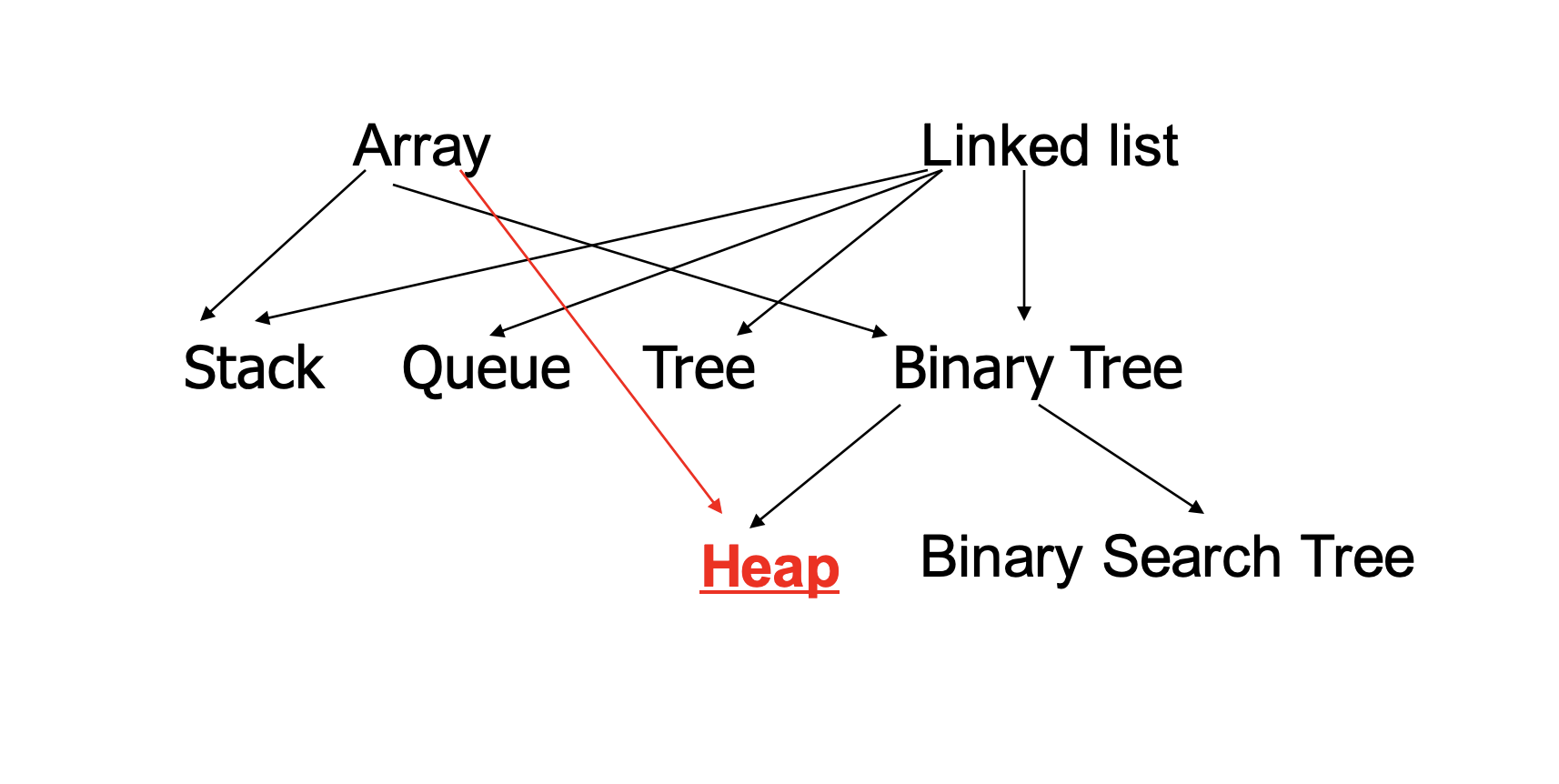
Priority Queue
- Queue
- Queue에 삽입된(도착 시간) 순서에 기반을 둠
- FIFO 혹은 FCFS 기반의 서비스 제공
- Priority(우선순위) Queue
- 더 일반적인 우선 순위에 기반을 둠
- 우선 순위의 예 : 직급, 중요도, 긴급도, 수행시간, 등
- (도착한 순서에는 상관없이) 우선 순위에 근거하여 서비스 제공
- 응용 예 :
- Job scheduling (OS)
- Military, Emergency
- Priority Queue : Find_Max (Min)
- Queue의 각 element는 priority 값 (Key 라고 지칭)을 가짐.
- Priority (혹은 key)는 보통 정수(integer) 값으로 표현.
- 가장 큰 정수 값 (예: 중요도)을 갖는 element가 먼저 delete 되는 경우, 이를 Max Priority Queue라고 함.
- 가장 작은 정수 값 (예: 수행시간)을 갖는 element가 먼저 delete 되는 경우, 이를 Min Priority Queue라고 함.
- 즉, Priority Queue의 핵심은 Maximum (혹은 Minimum) 값을 갖는 key를 찾는 문제.
Priority Queue의 구현
- Unordered Array
- Ordered Array
- Unordered Linked List
- Ordered Linked List
- Binary Search Tree
- Max Heap (Min Heap)
- Unordered Array를 이용
- Priority 값에 상관없이 Key들이 무작위(random)으로 저장.
- Delete 연산은 매우 비효율적; O(n)
- 처음부터 마지막까지 다 찾아봐야 함.
- Linear Search를 이용함.
- Insert 연산은 매우 효율적; O(1)
- 새로운 key를 무조건 array의 맨 끝에 넣으면 됨.
- 데이터 이동이 발생하지 않음.
- Ordered Array를 이용
- Priority 값을 기준으로 key들을 오름차순으로 정렬
- Priority 값이 가장 큰 key는 항상 array의 맨 끝에 위치함.
- Delete 연산은 매우 효율적; O(1)
- Insert 연산은 매우 비효율적; O(n)
- 새로운 key를 삽입할 때 항상 올바른 위치를 찾아서 넣어야 함. 이는 정렬상태를 유지해야 하기 때문.
- Binary Search를 이용하여 삽입 위치를 찾음; O(log2n)
- 삽입 후에 데이터 이동을 해야 함; O(n)
- Unordered Linked List를 이용
- (가정) ptr이라는 linked list의 맨 앞을 가리키는 pointer가 존재.
- Priority 값에 상관없이 Key들이 무작위(random)으로 저장.
- Delete 연산은 매우 비효율적; O(n)
- 처음부터 마지막까지 다 찾아봐야 함.
- Linear Search를 이용함; O(n)
- Insert 연산은 매우 효율적; O(1)
- 새로운 key 값을 list의 항상 맨 앞에 삽입
- 데이터 이동 발생하지 않음
- Ordered Linked List를 이용
- Priority 값을 기준으로 key들을 내림차순으로 정렬
- Priority 값이 가장 큰 key는 항상 맨 앞 node에 위치함.
- Delete 연산은 매우 효율적; O(1)
- Insert 연산은 매우 비효율적; O(n)
- 새로 삽입되는 key 값을 올바른 위치에 넣어야 함.
- Binary Search를 사용하기가 어려움;
- 최악의 경우 맨 뒤에 삽입됨; O(n);
- Binary Search Tree를 이용
- Key들을 Binary Search Tree(BST)에 저장함.
- Delete 연산은 비효율적;
- 가장 큰 key를 찾기 위해, 오른쪽 방향으로 계속 내려감.
- 시간은 BST의 height이고, 성능은 BST의 모양에 좌우됨
- Worst : O(n), Average : O(log2 n)
- Insert 연산은 비효율적;
- 새로운 key 값이 항상 leaf node에 삽입됨.
- 시간은 BST의 height이고, 성능은 BST의 모양에 좌우됨
- Worst : O(n), Average : O(log2 n)
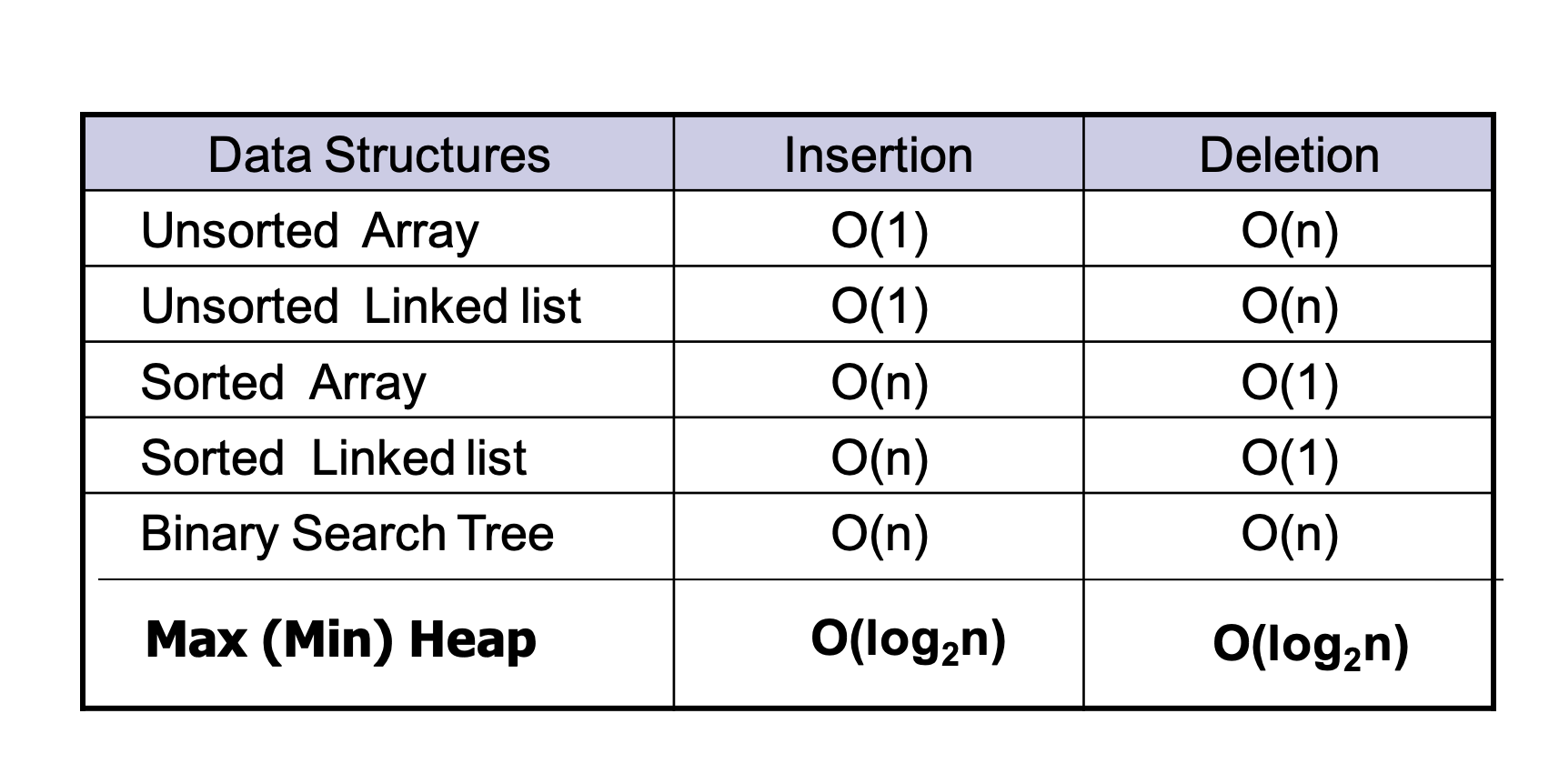
- Max(Min) Heap이 가장 효율적임. 삽입과 삭제 모두 O(log2n) 보장
- 예: n = 1,000일 경우 각 방법에 대해 시간 성능은? n = 1000,000?
Heap
- Max Heap :
- (1) Complete binary tree
- (2) Key of each node is no smaller than its children’s keys
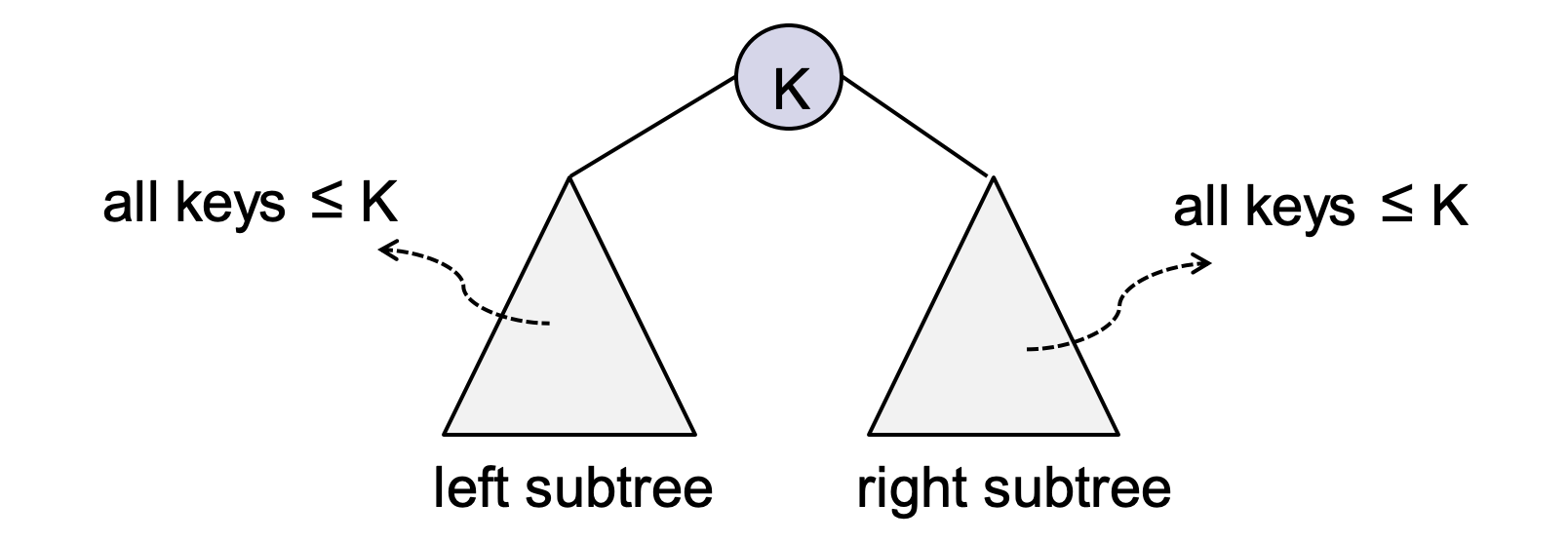
- Min Heap :
- (1) Complete binary tree
- (2) key of each node is no larger than its children’s keys.
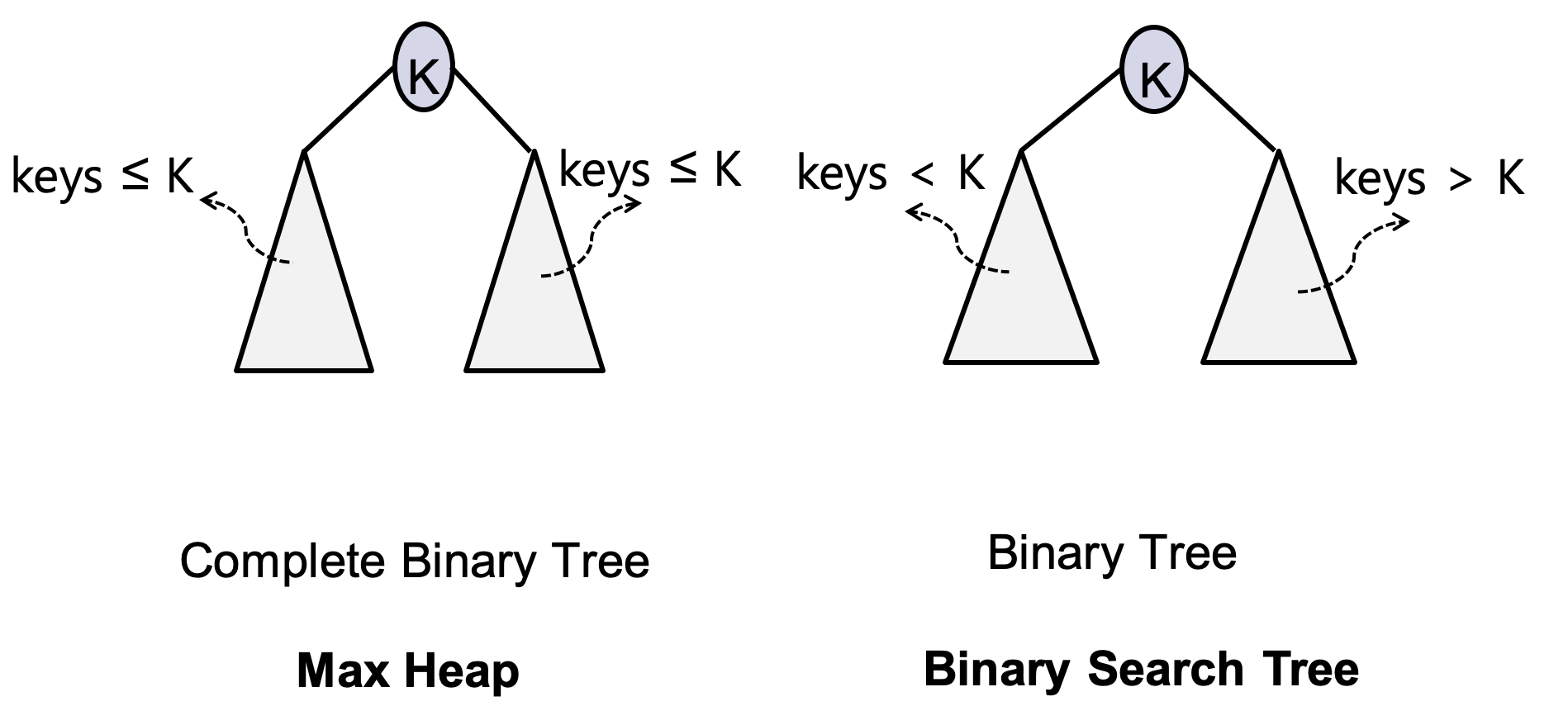
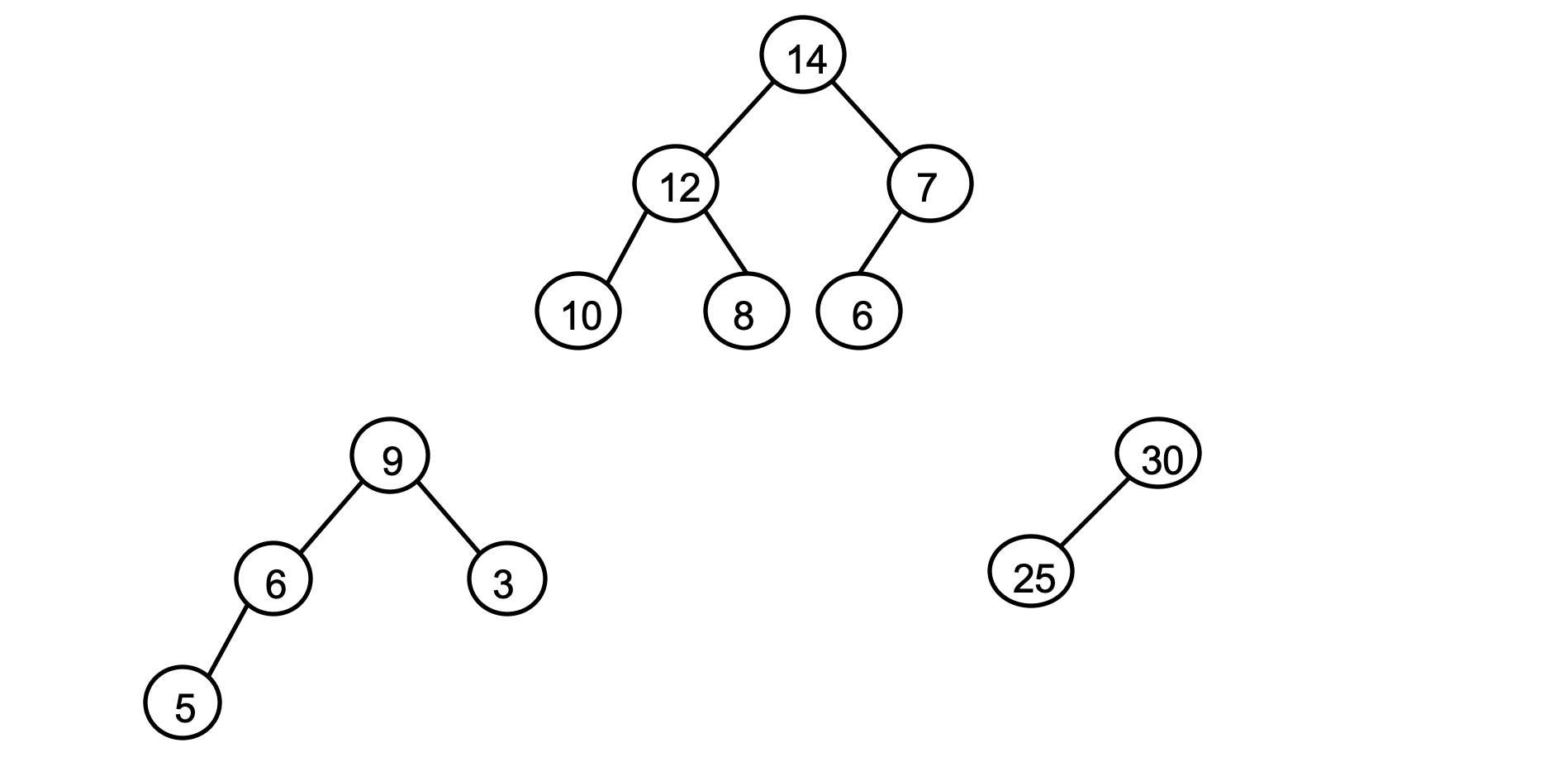
- Root of a max heap always has the largest value
- Examples : Not a Max Heap
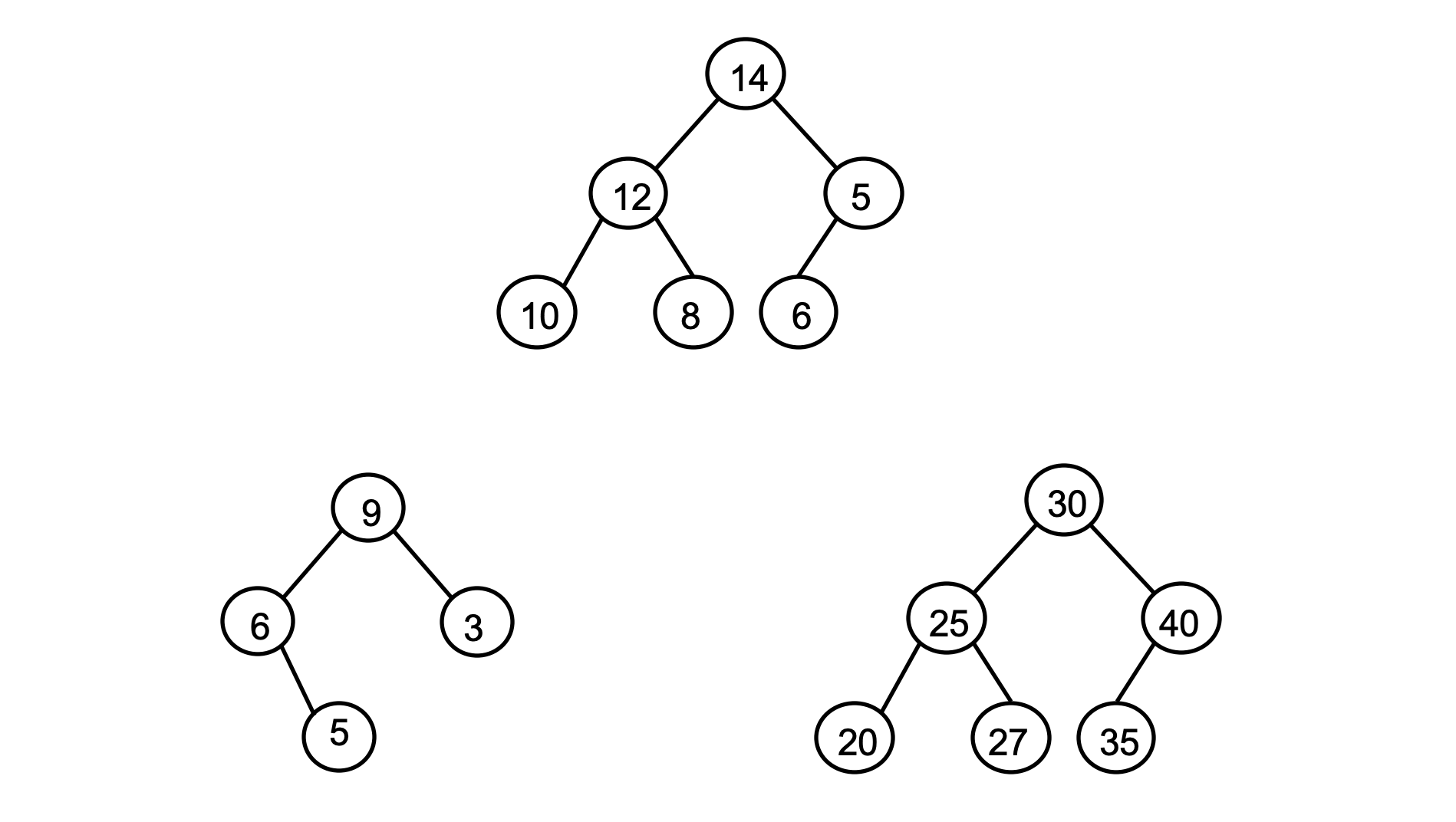

- Root* of a min heap always has the **smallest value.
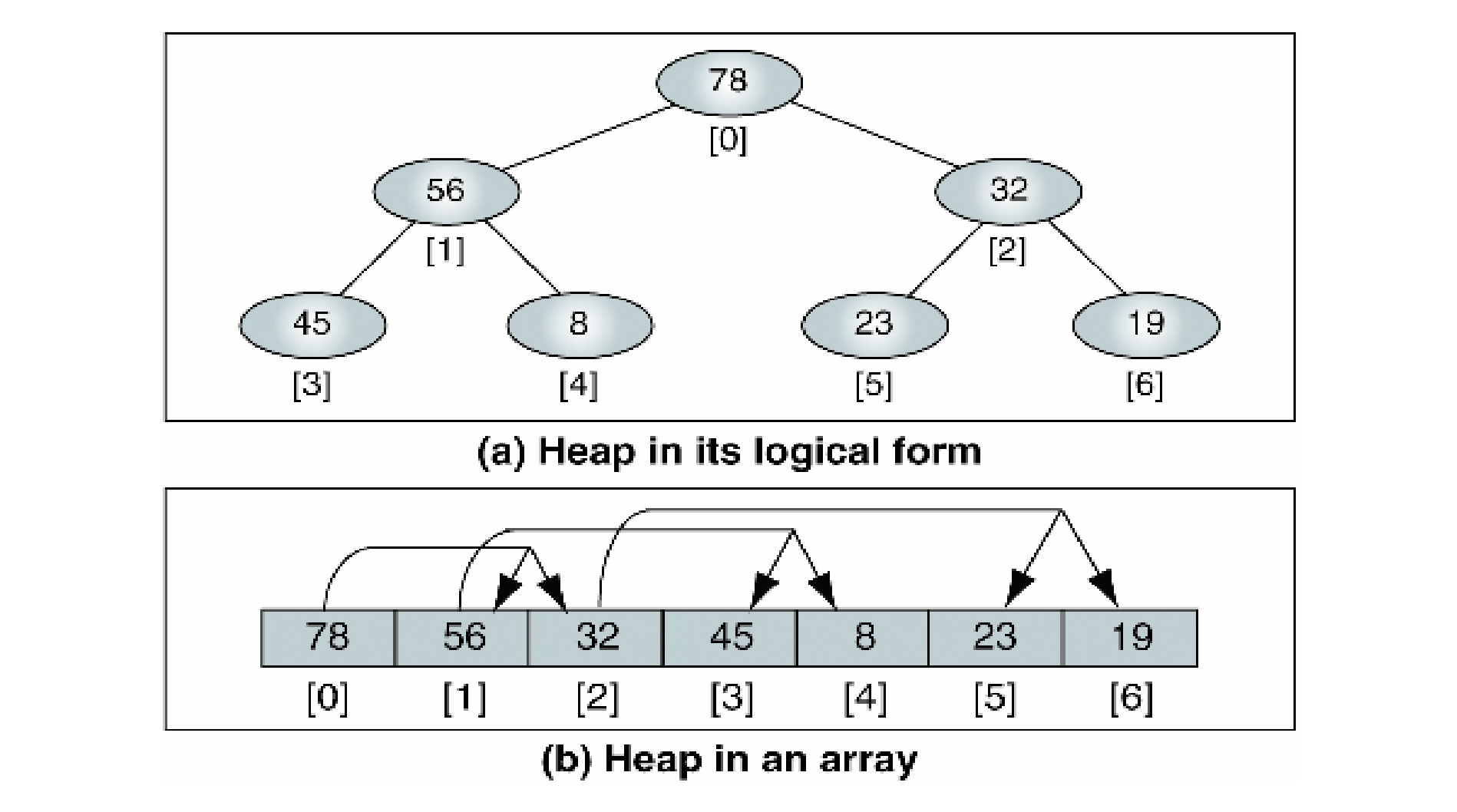
Heap : Array로 구현
- Heap을 array로 구현하는 이유
- (Complete binary tree 이므로) space 낭비가 없음.
- Parent와 child들의 위치를 찾기가 매우 쉬움
- Link list와 같은 복잡한 pointer 연산이 필요 없음.
- Finding a node location
- Left-Child(i) = 2i + 1
- Right-Child(i) = 2i + 2
- Parent(i) = $\lfloor$ (i - 1) / 2 $\rfloor$ (if i = 0, i is the root)
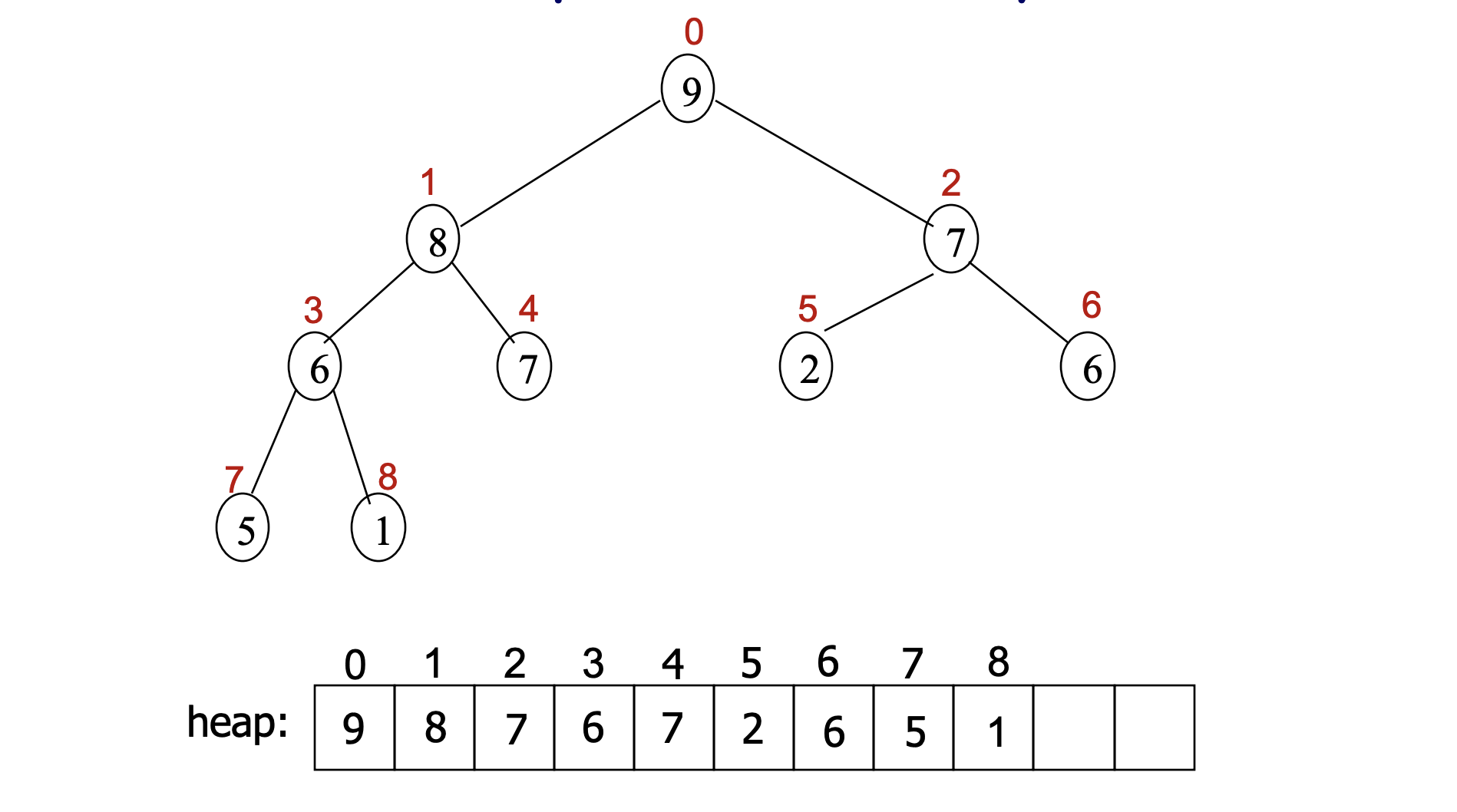
- heap에서 node 의 parent, left child, right child는?
Max (Min) Heap 연산
- Find-Max (Find-Min) : O(1)
- Largest (smallest) Key를 Max (Min) Heap에서 찾아 return;
- Insert : O(log2n)
- 새로운 key를 Max (Min) Heap에 삽입
- Delete : O(log2n)
- Largest (smallest) Key를 Max (Min) Heap에서 찾아 삭제;
- Sort : O(nlog2n)
- Key들을 올림 차순 (혹은 내림 차순)으로 정렬하여 출력
Insert : Max Heap
- Step 1 :
- (1) Insert a new key into max heap;
- (2) Insert 위치는? : 마지막 leaf node 바로 다음의 빈 공간;
- (Why? : condition (1)을 만족하기 위해)
- Step 2 :
- (1) Compare the new key with its parent;
- (2) If it is larger than the parent, swap it with the parent.
- Repeat step 2 until heap condition (2) is satisfied.
- Step 2 is called Reheap-Up
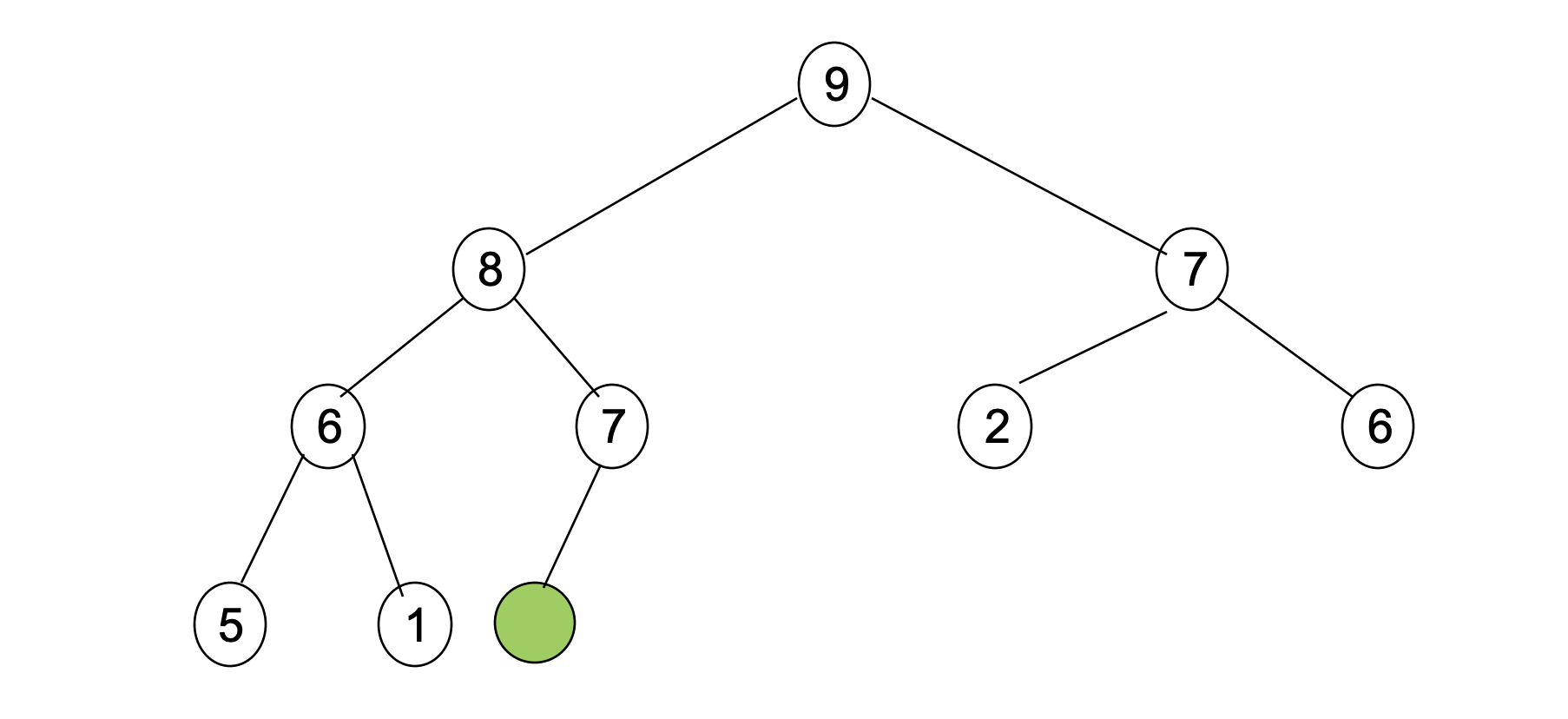
- Find an empty location; This is a node which is right next of the last leaf node.
Case 1
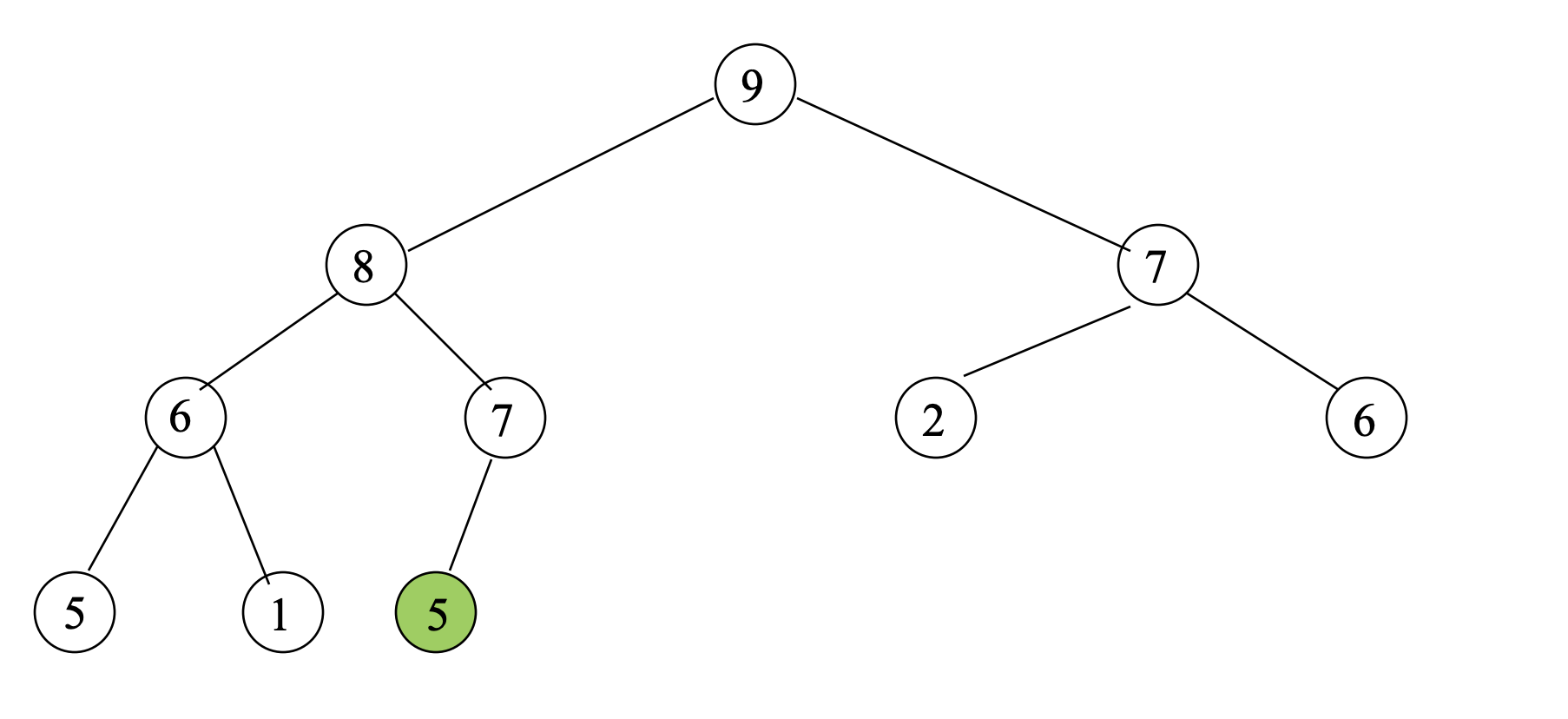
- Suppose we insert 5;
- This case is very simple; Just insert it.
Case 2
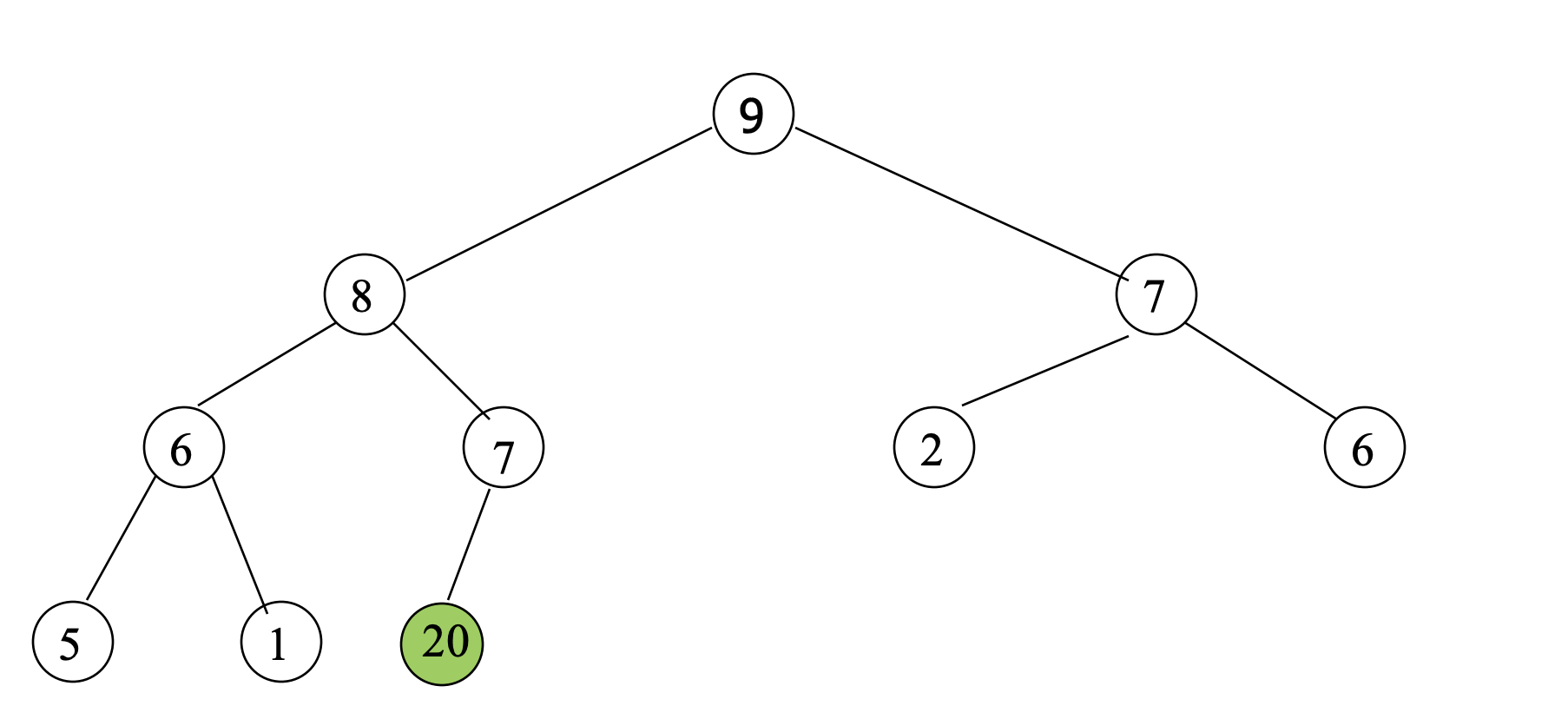
- Suppose we insert 20.
- Compare 20 with its parent (7).
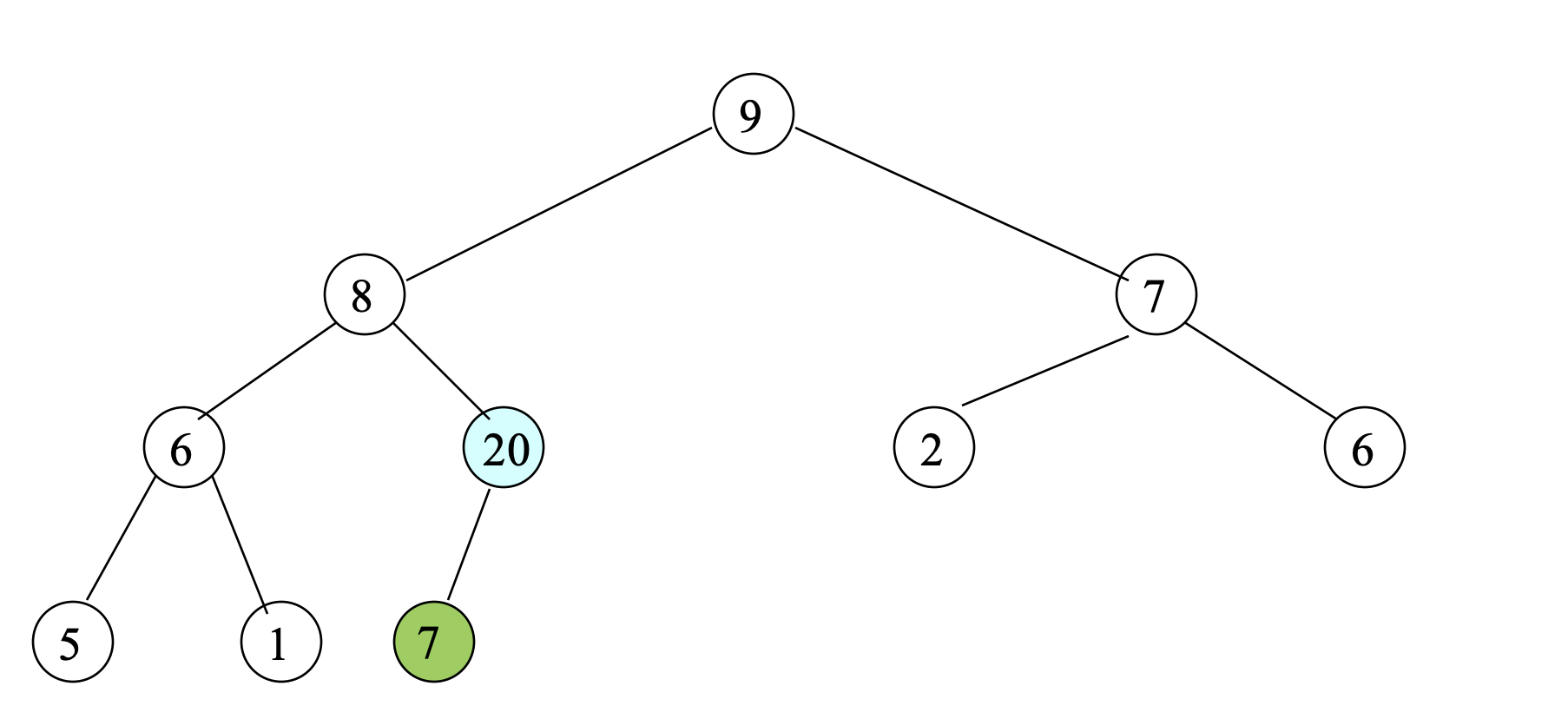
- Since 20 > 7, swap 20 and 7; 즉, Move 20 Up.
- Compare 20 with its parent (8).
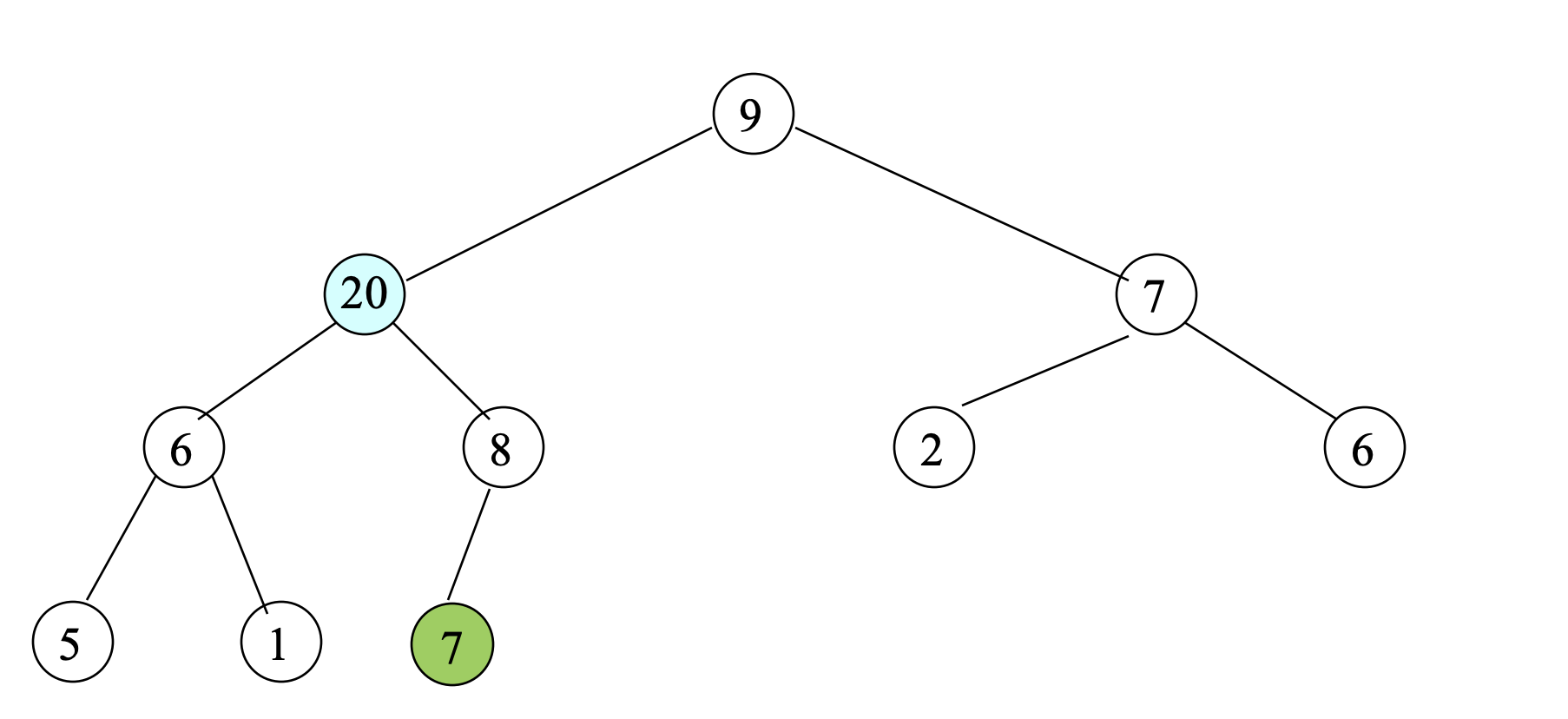
- Since 20 > 8, swap 20 and 8; 즉, Move 20 up again.
- Compare 20 with its parent (9).
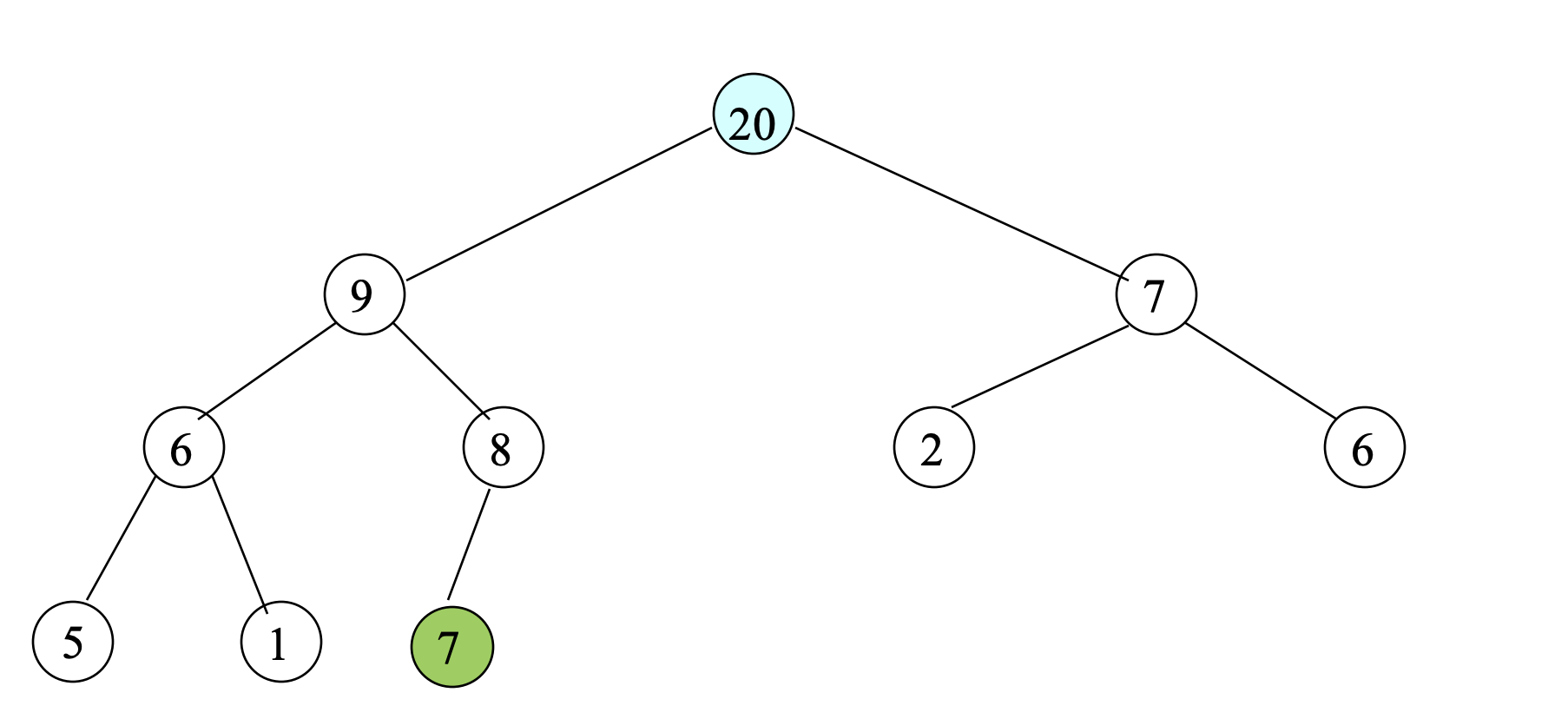
- Since 20 > 9, swap 20 and 9; Move 20 up again.
- Since this node is root, the insertion is done.
Delete : Max Heap
- Step 1 :
- (1) Find largest key and remove it.
- (2) Largest key는 항상 root에 있음; (remove 순간, root는 empty)
- Step 2 :
- (1) Find a key (say, L) in last leaf node and insert L into root.
- (2) Delete the last leaf node.
- Step 3 :
- (1) Compare L with its children.
- (2) If one of children is larger, swap L with the larger child.
- Repeat step 3 until heap condition (2) is satisfied.
- Step 3 is called Reheap-Down
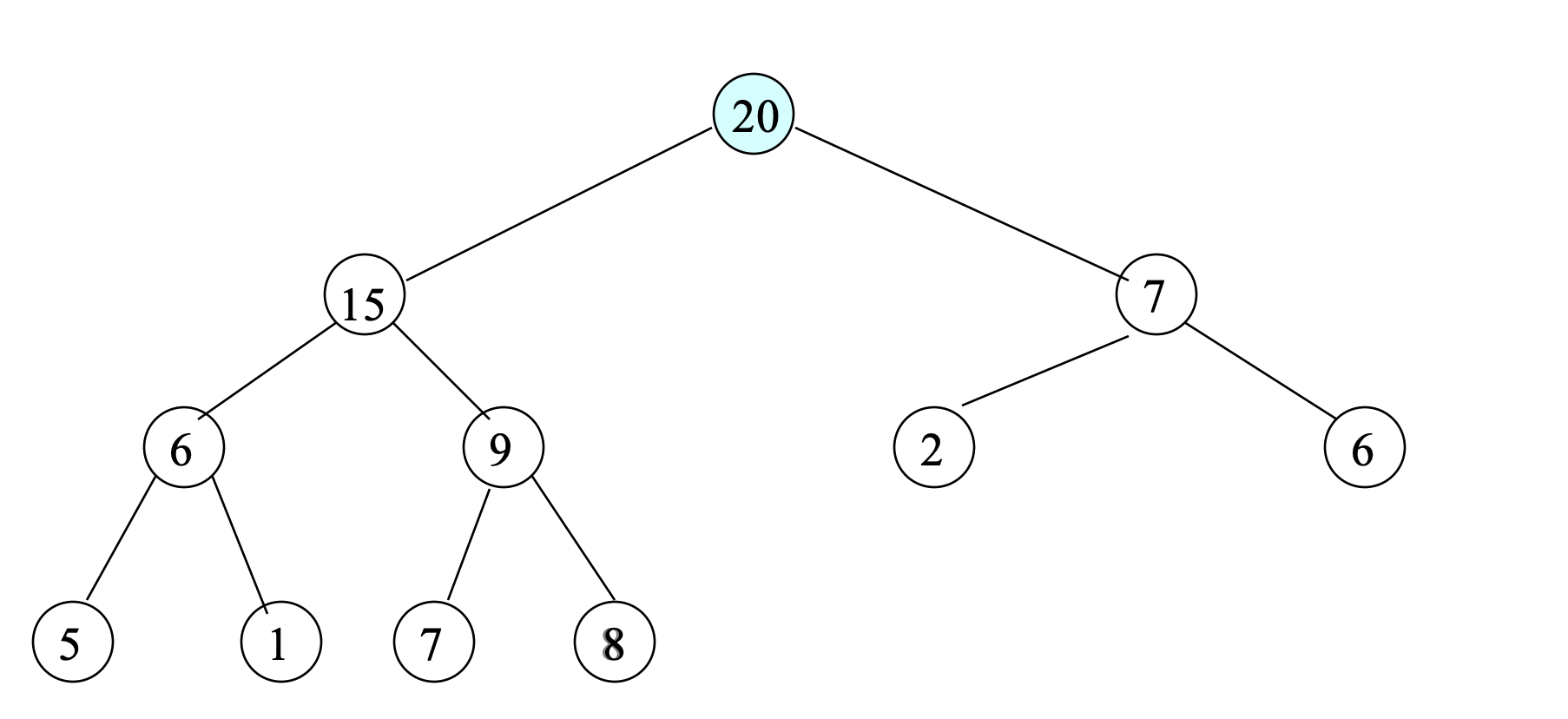
- Find the largest key;
- This key (20) is always in the root.
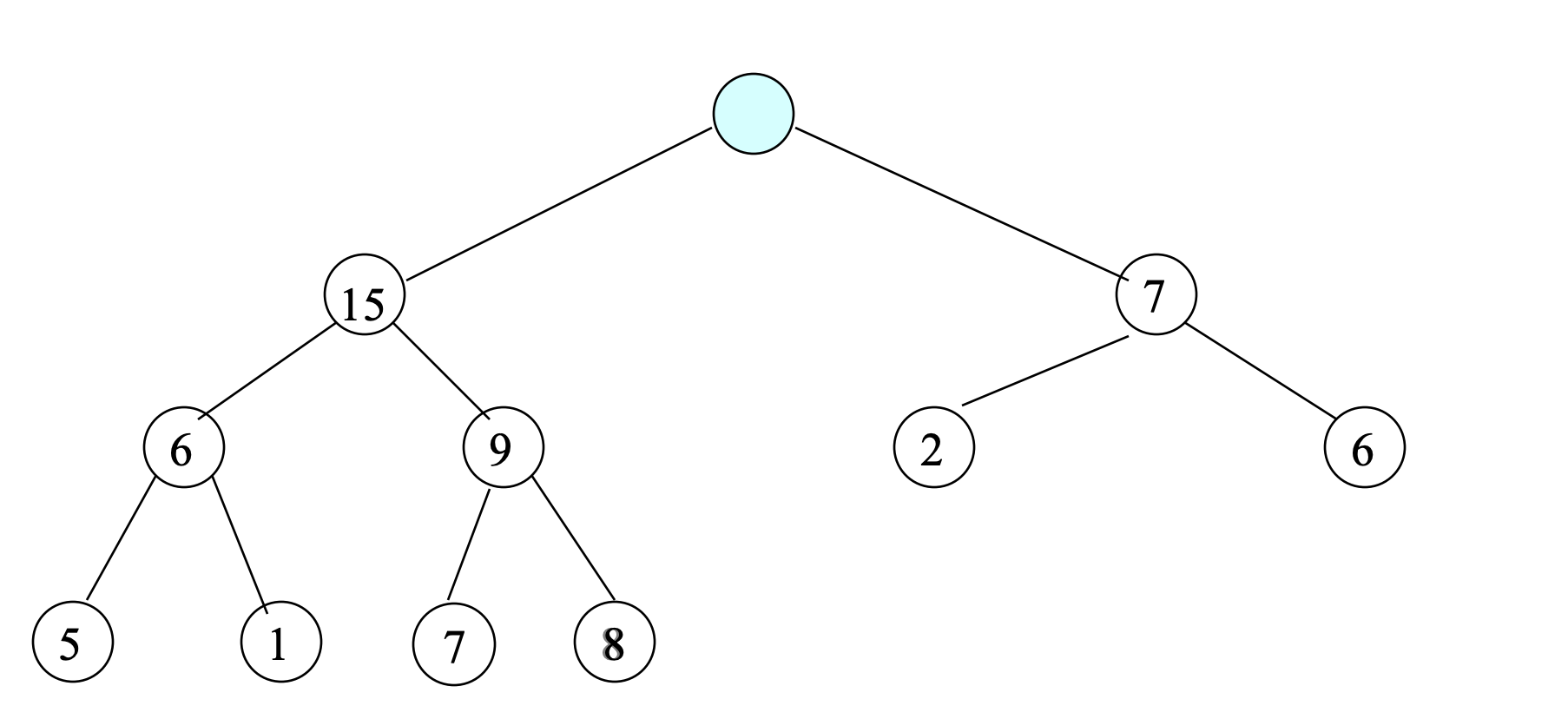
- After largest key (20) is removed, root is empty
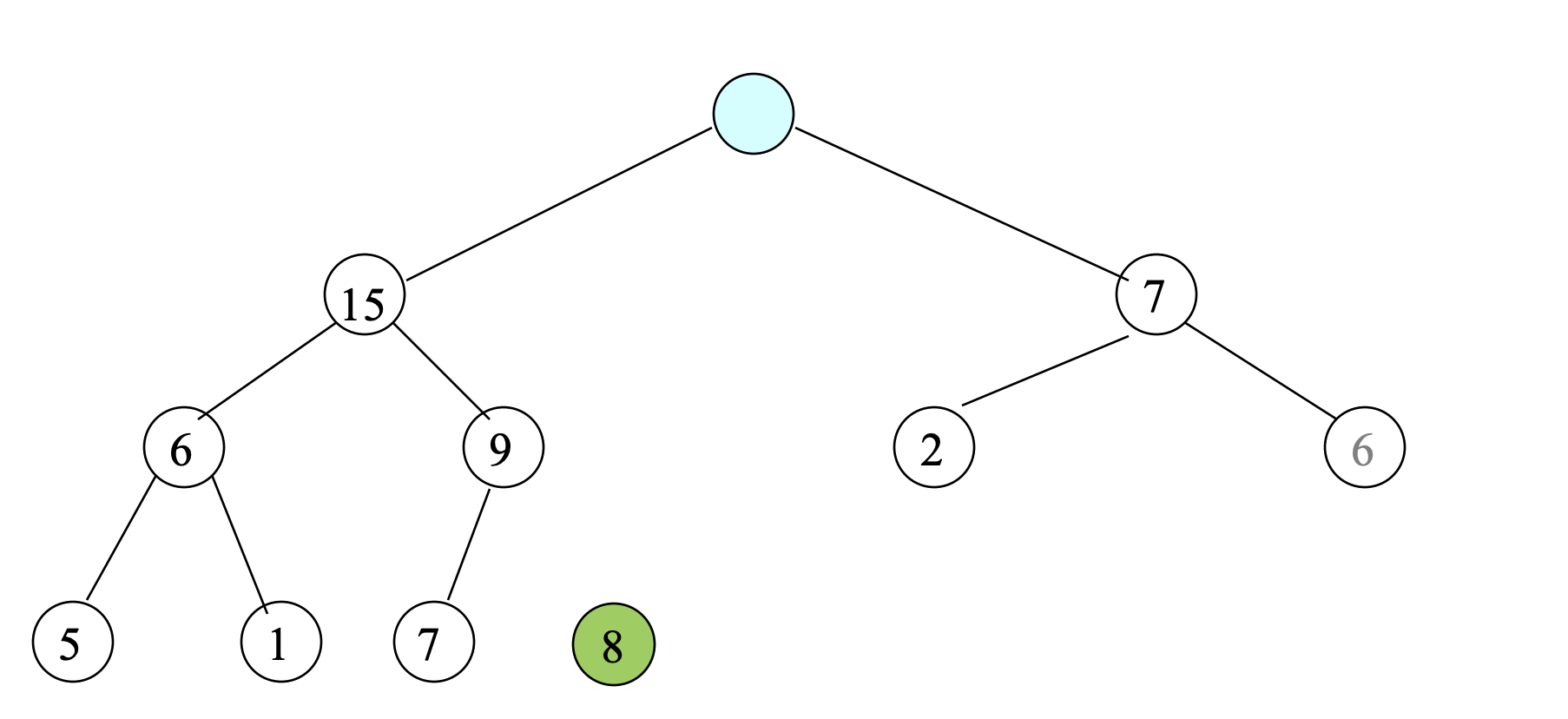
- Find the last leaf node; This contains 8.
- Delete this node from a heap; Then, there are 10 nodes
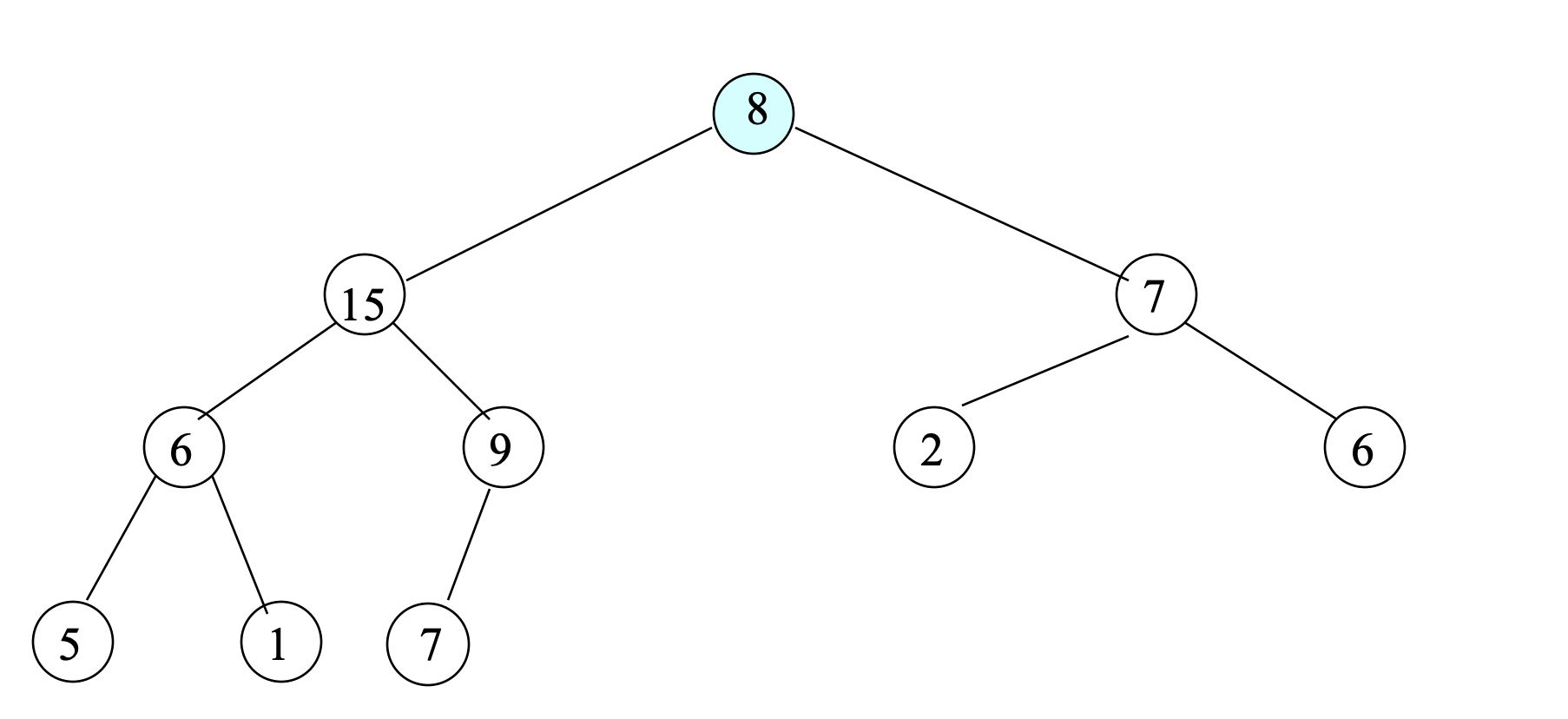
- To reinsert 8 into the heap, initially, store 8 at the root.
- Compare 8 with its child node with larger value; This is 15
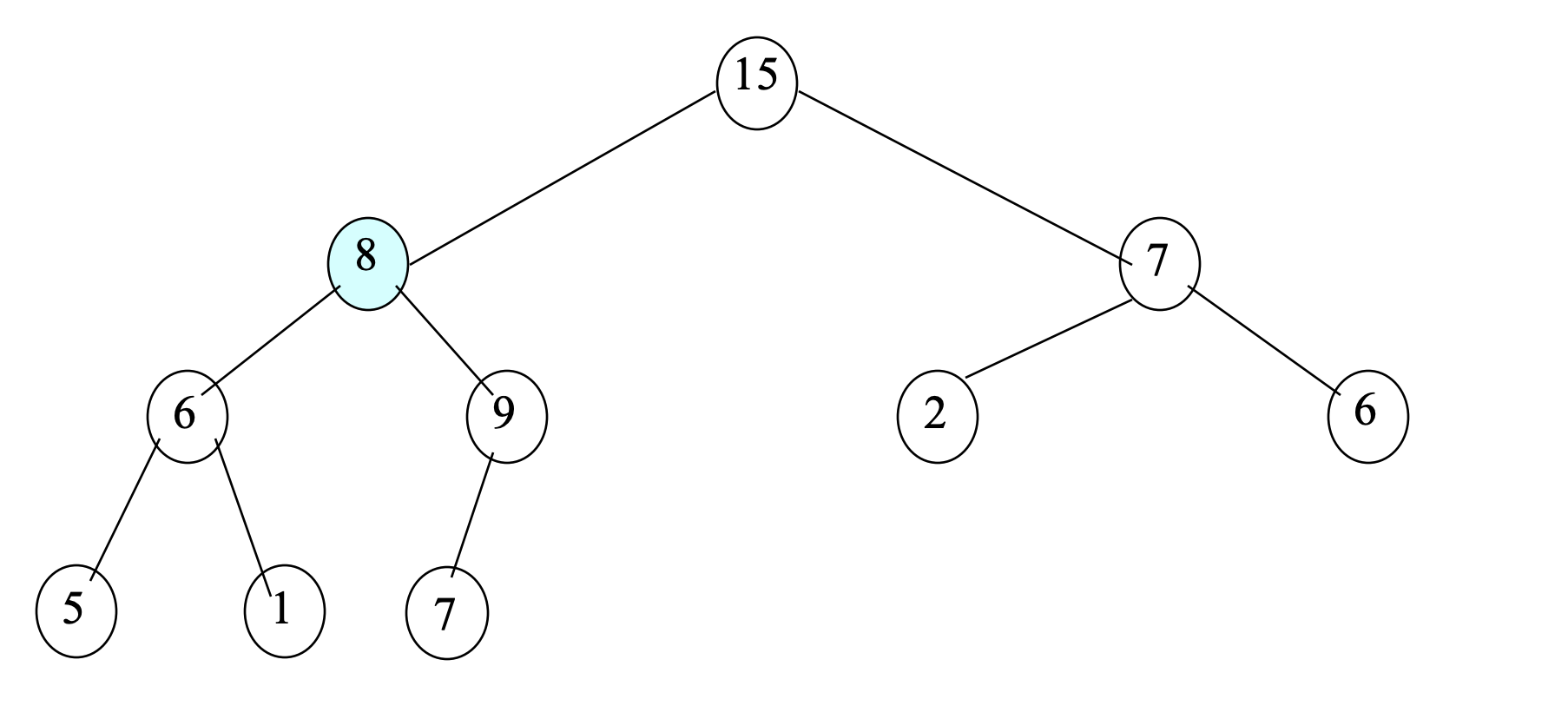
- Since 8 < 15, swap 8 and 15; Move 8 down.
- Compare 8 with its child node with larger value; This is 9.
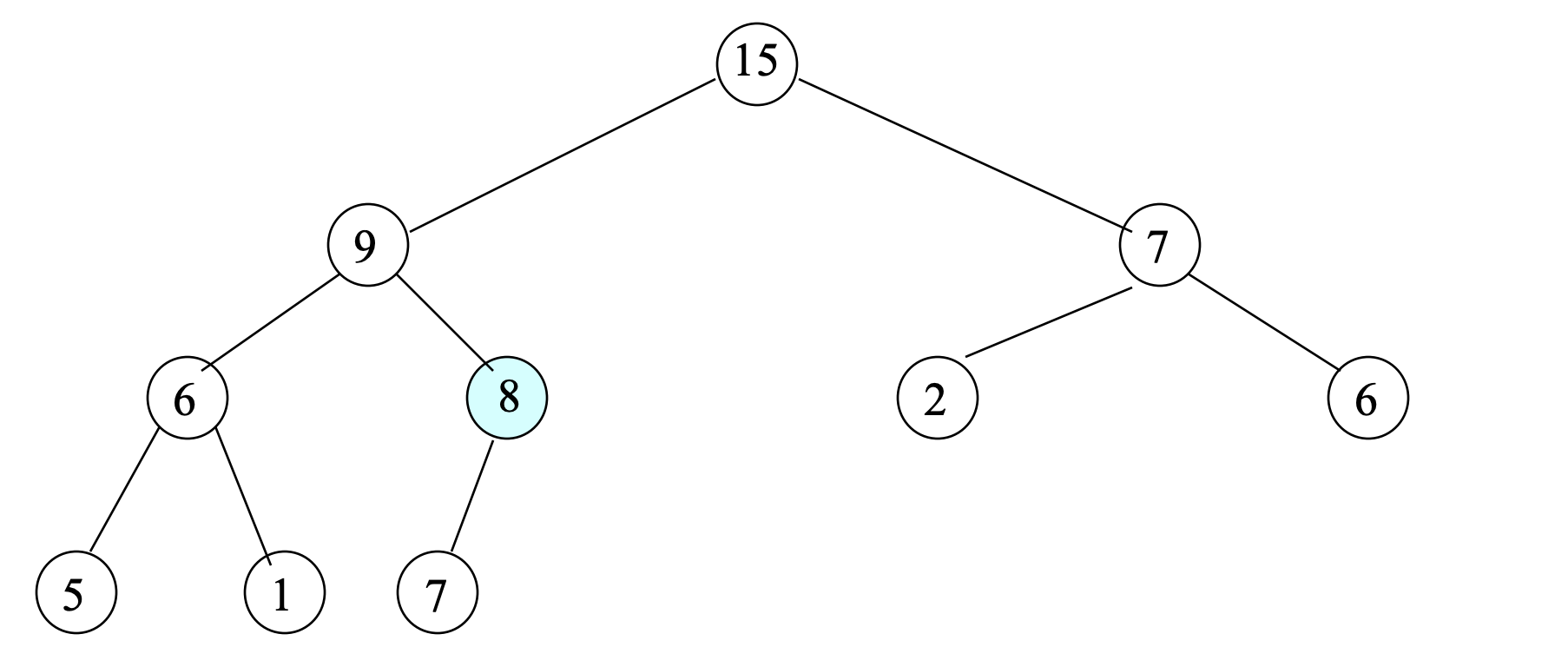
- Since 8 < 9, swap 8 and 9; Move 8 down.
- Compare 8 with its child node with larger value; This is 7.
- Since 8 < 7, the deletion is done
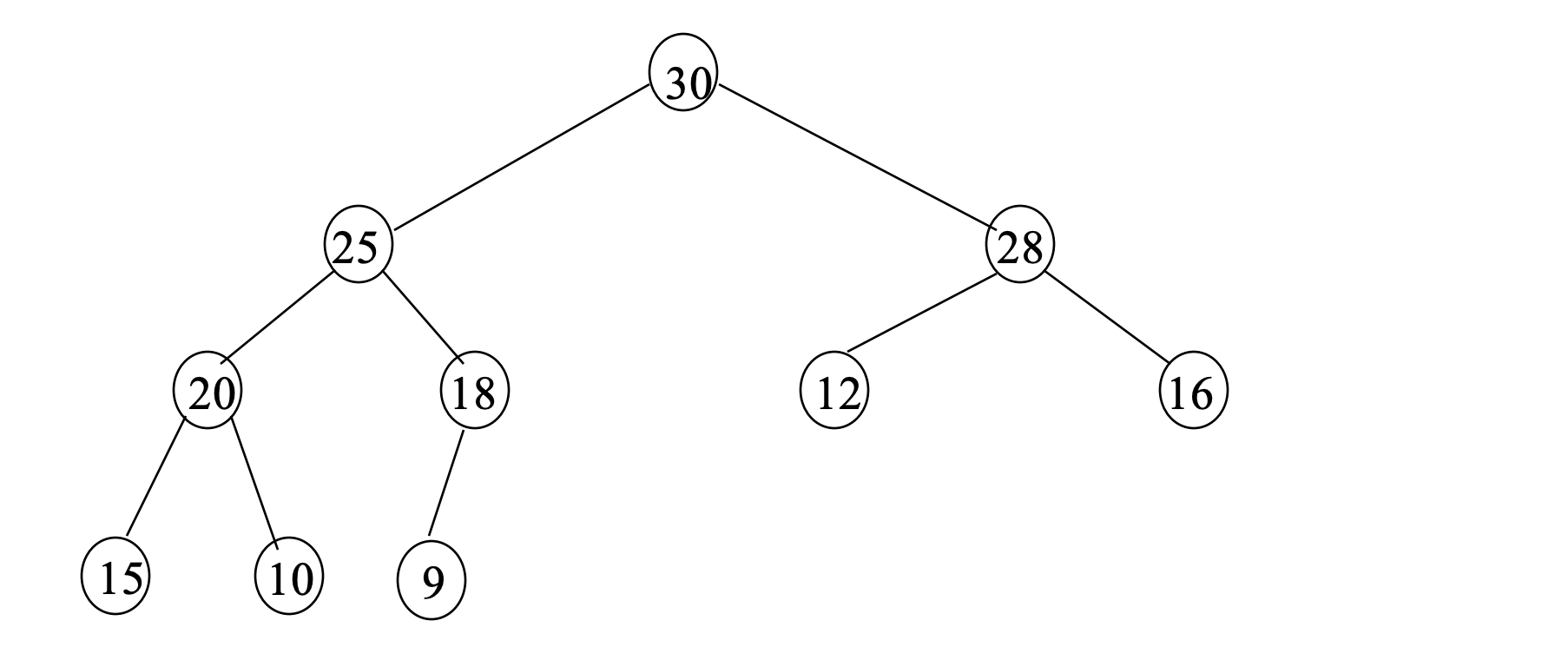
- 1) 위의 Max Heap을 array로 표현하라.
- 2) 위의 Max Heap에서 3번 연속 delete한 후 상태를 array는?
시간 분석 : Insert/Delete
- Insertion / deletion time is bounded by height of a heap.
- What is a height of heap? : O(log2n)
- 높이가 h인 Heap에서 node들의 최대/최소 개수는?
- (특히) Binary tree의 모든 각 node에서 왼쪽 subtree와 오른쪽 subtree의 높이 차이가 1 이하이면, 이를“Balanced” 라 함.
- 모든 Balanced Binary tree의 높이는 항상 log2 (n+1).
- Complete binary tree는 이러한 것들의 대표적인 유형.
Max Heap 응용 : Sort
- Max Heap을 이용하여 n 개의 key들을 올림 차순으로 sort하라.
- 예 : {40, 35, 20, 45, 60, 30, 25}
- 알고리즘(스케치):
- 1) Build a max heap from unsorted array;
- 2) Delete (the largest key) from max heap;
- 3) Put it at the end of array
- Repeat 2) and 3) n times
- 위 알고리즘의 시간 분석을 하라.
Max Heap : 연습
- Find $k^{th}$ largest key from an unsorted array with size n;
- 방법 1 : Sort and select element at location k
- 방법 2 : Build max heap and delete k times
- : 위 각 방법에 대해 시간 분석을 하여라.
- 다음의 key들을 차례대로 insert한 후의 max (혹은 min) heap을 array 상태로 단계별로 보여라.
- 예시 1 : {20, 25, 10, 30, 15, 35, 40, 45}
- 예시 2 : {10, 15, 20, 25, 30, 35, 40, 45}
- 예시 3 : {45, 40, 35, 30, 25, 20, 15, 10}
























댓글남기기